前言
众所周知,当我们在进行数组查找时,通常会碰到较多的数据,使用普通的遍历可能会使时间复杂度达到0(n²),处理起来十分麻烦,因此我们在这里引入时间复杂度为o(1)的哈希表。
解释
“哈希”,就是指高维到低维的映射,通常来说就是数据大的空间对数据小的空间的映射,在C++中,我们使用unordered_map<>来引用。
应用
先来看看题目:
给定一个整数数组 nums 和一个整数目标值 target,请你在该数组中找出 和为目标值 target 的那 两个 整数,并返回它们的数组下标。
你可以假设每种输入只会对应一个答案。但是,数组中同一个元素在答案里不能重复出现。
你可以按任意顺序返回答案。
示例 1:
输入:nums = [2,7,11,15], target = 9 输出:[0,1] 解释:因为 nums[0] + nums[1] == 9 ,返回 [0, 1] 。
示例 2:
输入:nums = [3,2,4], target = 6 输出:[1,2]
示例 3:
输入:nums = [3,3], target = 6 输出:[0,1]
提示:
2 <= nums.length <= 104-109 <= nums[i] <= 109-109 <= target <= 109- 只会存在一个有效答案
进阶:你可以想出一个时间复杂度小于 O(n2) 的算法吗?
对于这题,我们很容易想到利用两个for循环来进行查找,但这样的时间复杂度太高
For循环(时间复杂度o(n²))
class Solution {
public:
vector<int> twoSum(vector<int>& nums, int target) {
int n = nums.size();
for (int i = 0; i < n; ++i) {
for (int j = i + 1; j < n; ++j) {
if (nums[i] + nums[j] == target) {
return {i, j};
}
}
}
return {};
}
};提交结果:
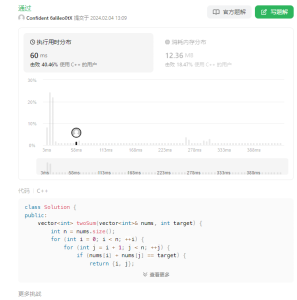
仅仅在前40%
但当我们使用哈希表时:
哈希表(时间复杂度o(1))
class Solution {
public:
vector<int> twoSum(vector<int>& nums, int target) {
unordered_map<int,int> h;
vector <int> ret(2);
for(int i=0,I=nums.size();i<I;++i){
if(h.find(target-nums[i])!=h.end()){
ret[0]=h[target-nums[i]];
ret[1]=i;
break;
}
h[nums[i]]=i;
}
return ret;
}
};提交结果:
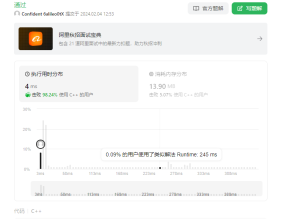
可以看到运行速度在前1%
由此可以看出哈希表的强大之处。

评论(0)
暂无评论